[Algorithm] 되추적, 역추적 (Backtracking) - N Queen문제

Backtracking (되추적, 역추적)

• 문제의 제약 조건을 충족하지 못하는 솔루션을 제거하여 반복적으로 문제를 해결하는 알고리즘 기술
• recursive 를 사용하여 문제를 해결
• 최적화 문제를 해결하기 위해 가능한 모든 조합을 찾으려면 역 추적이 필요하다고 할 수 있음
• Backtracking 은 효과적인 결정을 찾을 때까지 다양한 결정 순서를 시도하는 체계적인 방법
• 모든 경우의 수를 상태공간 트리를 통해 표현
• DFS( depth-first search ) 을 이용하여 해결
• Promising : 해당 루트가 조건에 맞는지 검사
• Pruning : 조건에 맞지 않는 경우, 다른 루트로 가서 탐색 시간 절약

• 녹색은 시작점, 파란색은 중간 점, 빨간색은 실행 가능한 솔루션이없는 점, 진한 녹색은 최종 솔루션
• 끝까지 진행되어 솔루션인지 아닌지 확인하고, 그렇지 않으면 솔루션을 반환
• 솔루션을 찾기 위한 다음 지점으로 트랙을 찾기 위해, 한 단계 뒤의 지점으로 역 추적하여 진행 됨

대표적인 문제들

• N Queen
• Maze
• Sudoku
• Hamiltonian Circuit
• Subset Sum

N Queen

• N-Queens 문제는 동일한 행, 열 또는 대각선에있는 여왕이 서로를 공격하지 않도록 n-여왕을 nxn 체스 판에 배치하는 것

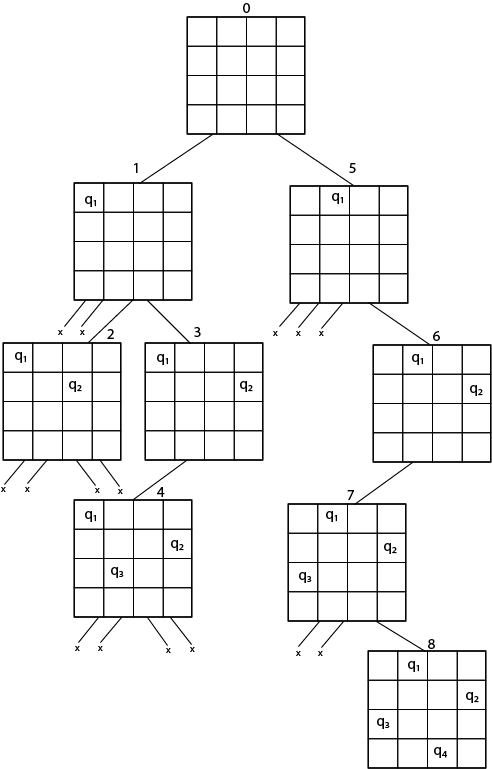
{0, 1, 0, 0}
{0, 0, 0, 1}
{1, 0, 0, 0}
{0, 0, 1, 0}

• 재귀 용법으로 찾는 8 퀸문제

---

references

https://www.javatpoint.com/backtracking-introduction
https://www.javatpoint.com/n-queens-problems
https://www.geeksforgeeks.org/backtracking-algorithms/
https://www.geeksforgeeks.org/java-program-for-n-queen-problem-backtracking-3/ https://www.tutorialspoint.com/introduction-to-backtracking
https://ko.wikipedia.org/wiki/%EC%97%AC%EB%8D%9F_%ED%80%B8_%EB%AC%B8%EC%A0%9C