[Algorithm] 분할 정복 (Divide and Conquer)

Divide and Conquer (DAC : 분할 정복)

• 문제를 더이상 나눌 수 없을 때까지 나누고, 나누어진 문제를 각각 개별적으로 풀어 전체 문제에 대한 답을 얻는 알고리즘
• 장점 : 문제를 나누어 풀기 때문에 성능 우수
• 단점 : 재귀 함수를 사용하기 때문에 비용 문제 발생

연산

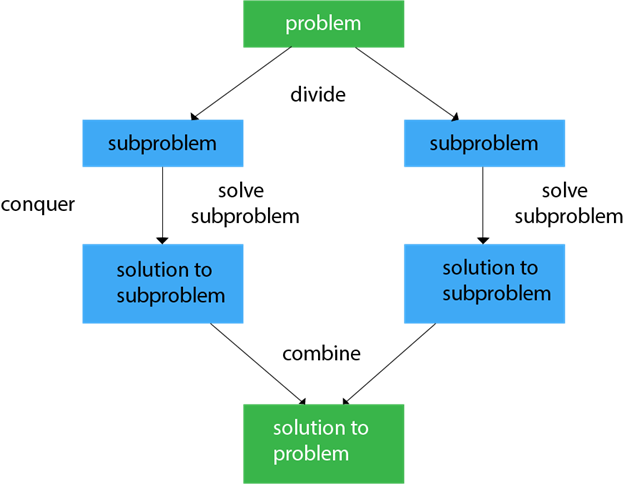
1. Divide 분할 : 원래 문제를 하위 문제로 나눔 (하위 문제의 집합 = 원래의 문제)
2. Conquer 정복 : 모든 하위 문제를 개별적으로, 재귀 적으로 해결
3. Combine 결합 : 하위 문제의 솔루션을 모아 전체 문제에 대한 솔루션을 얻음

종류

• Merge Sort (병합 정렬)
• Quick Sort (퀵 정렬)
• Binary Search (이진 검색)
• Tower of Hanoi (하노이의 탑)
• Strassen’s Matrix Multiplication (슈트라센 알고리즘)
  • Strassen의 알고리즘 은 두 행렬을 곱하는 효율적인 알고리즘
  • 두 행렬을 곱하는 간단한 방법은 3 개의 중첩 루프가 필요하며 O (n³)
  • Strassen의 알고리즘은 O (n^2.8974) 시간에 두 개의 행렬을 곱함
• Closest pair (points) (최근접 점쌍 문제)
  • 가장 가까운 점 쌍 문제는 xy 평면의 점 집합에서 가장 가까운 점 쌍을 찾는 문제
  • 이 문제는 모든 점 쌍의 거리를 계산하고 거리를 비교하여 최소값을 구함으로써 O (n²) 시간 내에 해결할 수 있음

complexity

• 시간복잡도 : O(nLogn)

자바를 이용하여 divide and conquer - fibonacci 수열 구현 (재귀함수 사용)

전체소스보기

public static int fibonacciRecusrion(int n) {
    if(n < 2) {
        return n;
    }else{
        return fibonacciRecusrion(n-1) + fibonacciRecusrion(n-2);
    }
}

---

references

https://www.javatpoint.com/divide-and-conquer-introduction
https://www.geeksforgeeks.org/divide-and-conquer-algorithm-introduction/
https://www.tutorialspoint.com/data_structures_algorithms/dynamic_programming.htm