[Algorithm] 탐욕 알고리즘 (Greedy Algorithm)

Greedy Algorithm (탐욕 알고리즘)

• 최상의 옵션을 선택하는 알고리즘
• 솔루션을 하나씩 구축하는 알고리즘 패러다임
• 최상의 출력을 제공 할 수도 있고 제공하지 않을 수도 있음

연산

• 선택을 해야하는 특정 순간 가장 좋은 방법 / 옵션을 찾아 선택하는 알고리즘

종류

• Huffman code (허프만 코드)
• Travelling Salesman Problem (외판원 문제)
• Prim’s Minimal Spanning Tree Algorithm (프림의 최소 신장트리 문제)
• Kruskal’s Minimal Spanning Tree Algorithm (크루스칼의 최소 신장트리 문제)
• Dijkstra’s Minimal Spanning Tree Algorithm (다익스트라의 최소 신장트리 문제)
• Graph - Map Coloring
• Graph - Vertex Cover
• Job Scheduling Problem
• Machine scheduling
• Fractional Knapsack Problem (부분 배낭 문제)
• Activity Selection Problem (활동 선택 문제)

자바를 이용하여 탐욕알고리즘 - 동전선택문제(=거스름돈) 구현

1. 가치가 높은 동전을 선택
2. 동전을 더하여 총 금액을 초과하지 않을 만큼 각 동전의 필요 갯수 구하기

전체소스보기

public static int[][] countCoin(int amount, int[] arr) {

    int[] cointCount = new int[arr.length];
    int[][] result = new int[arr.length][2];

    int total = amount;

    for (int i = 0; i < arr.length ; i++) {
        if (total >= 0){
           //coin의 갯수가 들어감
           cointCount[i] = total/arr[i];

           //coinCount가 1개 이상일 경우
           if (cointCount[i] >= 1) {
               //남은 잔액을 계산후 반복
               total=total%arr[i];
               //현재 카운트 된 동전의 금액 : 갯수
               result[i][0] =  arr[i];
               result[i][1] =  cointCount[i];
           } //end if
       }
   }
   return result;
 }

output

-----  coin type :
[10, 100, 50, 500]
-----  after coin sort :
[500, 100, 50, 10]
----- amount : 4830
[500 : 9, 100 : 3, 0 : 0, 10 : 3]
-----  amount : 11670
[500 : 23, 100 : 1, 50 : 1, 10 : 2]

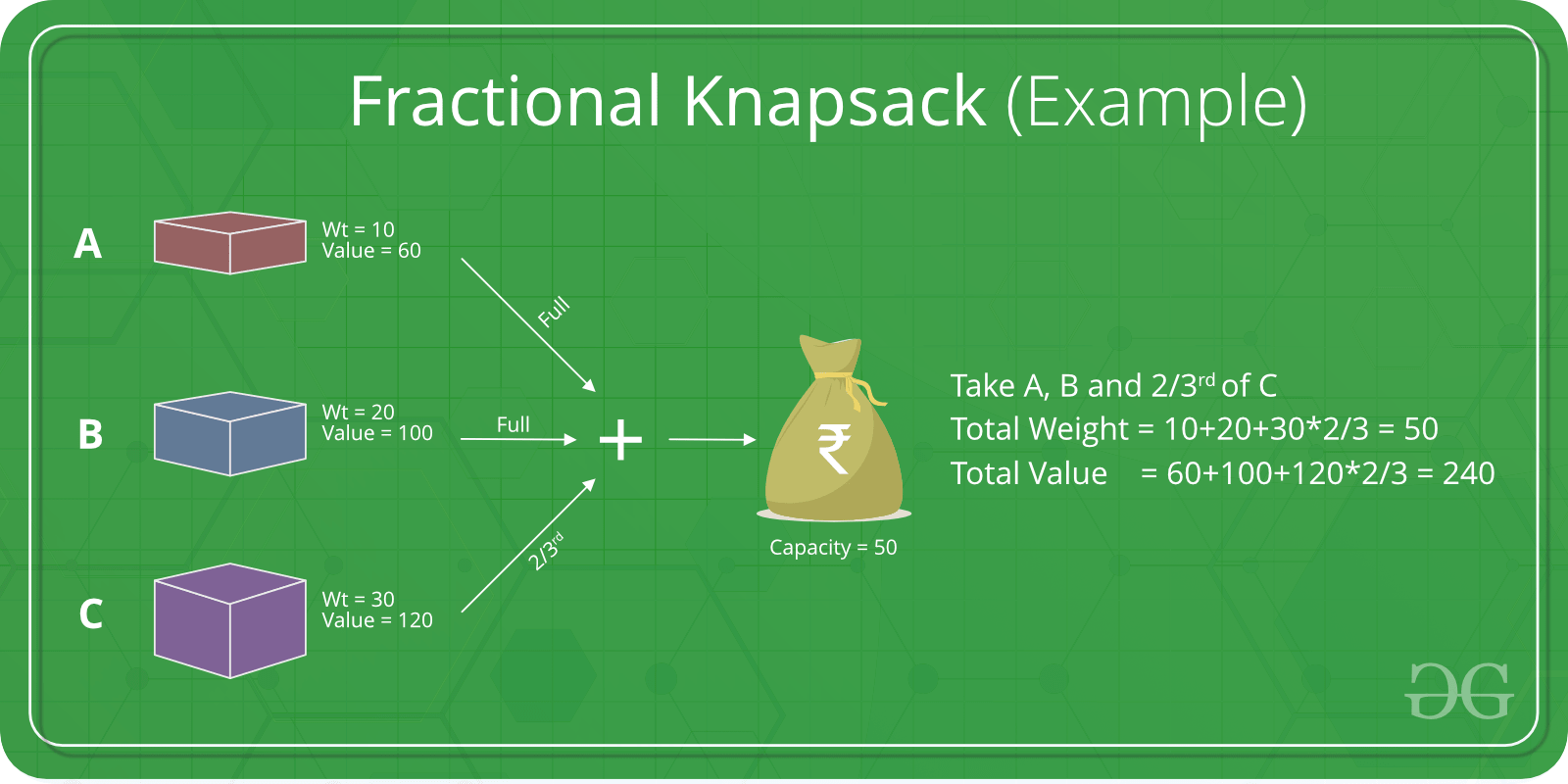
자바를 이용하여 탐욕알고리즘 - Fractional Knapsack Problem 부분 배낭 문제 구현

1. 배낭이 담을 수 있는 총 capacity에 딱 맞게 아이템을 담는 문제
2. 각 아이템의 무게 weight, 가치 value가 주어짐
3. cost = value/weight 로 계산해서 각 아이템의 가치를 측정
4. 가치가 높은 아이템 부터 담기
5. 아이템 한개를 온전히 담을 수 없을때까지 까지 반복
6. 아이템을 한개를 온전히 담을 수 없을땐 쪼개서 capacity채우기

전체소스보기

private static double getMaxValue(int[] weight, int[] value, int capacity) {

    ItemValue[] itemValue = new ItemValue[weight.length];

    //cost계산
    for (int i = 0; i < itemValue.length; i++) {
        itemValue[i] = new ItemValue(weight[i], value[i], i);
    }

    // cost를 기준으로 내림차순 정렬
    Arrays.sort(itemValue, new Comparator<ItemValue>() {

       @Override
       public int compare(ItemValue o1, ItemValue o2) {
           return o2.getCost().compareTo(o1.getCost());
       }
    });

    System.out.println(toString(itemValue));

    double totalValue = 0d;

    //cost 가 높은것부터 아이템 한개씩 꺼내서 계산
    for (ItemValue item : itemValue) {
        int currentWeigth = (int)item.weight;
        int currentValue = (int)item.value;

        //capacity가 아이템 한개를 다 담을 수 있을 때
        if( capacity - currentWeigth >= 0) {

            capacity = capacity - currentWeigth;
            totalValue  = totalValue + currentValue;
            System.out.println("total value : "  + totalValue + ", current weight : " +currentWeigth + ", current value : " + currentValue);

        } else {
            //아이템 한 개 를 다 담지 못하는 경우 쪼깸
            // 남은 용량/현재 무게
            double fraction = (double)capacity/(double)currentWeigth;

            capacity = (int)(capacity - (currentWeigth*fraction));
            totalValue  = totalValue + (currentValue * fraction);

            System.out.println("total value : "  + totalValue + ", current weight : " +currentWeigth + ", current value : " + currentValue + ", fraction :" + fraction);
            break;
        }
    }
        return totalValue;
    }

    static class ItemValue{
        private double weight, value, index;
        private double cost;

        public ItemValue(int weight, int value, int index) {
            this.weight = weight;
            this.value = value;
            this.index = index;
            //cost 계산
            cost = (value/weight);
        }

        public double getWeight() {
            return weight;
        }

        public double getValue() {
            return value;
        }

        public double getIndex() {
            return index;
        }

        public Double getCost() {
            return cost;
        }
    }

output

[ * FractionalKnapSack * ]
capacity :50
[index : 0, cost : 6.0, value : 60, weight : 10/ index : 2, cost : 5.0, value : 100, weight : 20/ index : 3, cost : 4.0, value : 120, weight : 30/ index : 1, cost : 1.0, value : 40, weight : 40]
total value : 60.0, current weight : 10, current value : 60
total value : 160.0, current weight : 20, current value : 100
total value : 240.0, current weight : 30, current value : 120, fraction :0.6666666666666666
Maximum value  = 240.0

---

references

https://www.javatpoint.com/greedy-algorithms
https://www.geeksforgeeks.org/greedy-algorithms/
https://www.tutorialspoint.com/data_structures_algorithms/greedy_algorithms.htm