[Algorithm] 최소신장트리 (MST) - 크루스칼(kruskal), 프림(Prim)
Minimum Spanning Tree (MST: 최소신장트리) - Kruskal(크루스칼), Prim(프림)
Spanning Tree 속성
- 최소 가장자리 수를 갖는 동일한 가중치의 Minimum Spanning Tree가 여러 개 존재 가능
- 주어진 그래프의 모든 간선 가중치가 동일하면 해당 그래프의 모든 스패닝 트리가 최소
- 각 모서리에 고유 한 가중치가있는 경우 고유 한 최소 스패닝 트리가 하나만 있음
- 연결된 그래프 G는 하나 이상의 스패닝 트리를 가질 수 있음
- 연결이 끊어진 그래프는 트리에 걸쳐있을 필요가 없거나 모든 정점에 걸쳐있을 수 없음
- 스패닝 트리에는 주기가 없음
- 스패닝 트리에는 (n-1) 개의 가장자리가 있는데, 여기서 n은 정점의 수
- 단일 에지를 하나만 추가하면 스패닝 트리가 비순환 성 속성을 잃고 하나의 단일 에지를 제거하면 연결 속성이 손실되어짐
- 그래프 G에서 연결선 일부를 사용하여 그래프의 모든 정점들이 연결되어 트리로 구성될 때
- 스패닝 트리는 모든 정점을 함께 연결하는 연결 및 무방향 그래프 G의 비순환 하위 그래프
- 그래프 G는 여러 개의 스패닝 트리를 가질수 있음
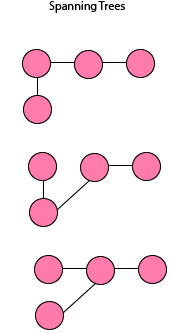
Minimal Spanning Tree (MST) : 최소생성 트리
- 최소 스패닝 트리는 최소 총 비용이 있는 스패닝 트리
- 가중치 (또는 비용)가있는 링크 된 무 방향 그래프가 각 모서리와 결합 된 경우
- 스패닝 트리의 비용은 가장자리 비용의 합계
- 사이클이 형성되면 안 됨
- 실제 상황에서이 가중치는 거리, 혼잡, 교통 부하 또는 가장자리에 표시된 임의의 값으로 측정
- 가중치 그래프에서 모든 모서리에 가중치를 지정 가능
- 최소 스패닝 트리는 총 가중치가 최소인 스패닝 트리
- 최소 스패닝 트리는 특정 그래프의 다른 모든 스패닝 트리 중에서 최소 가중치를 포함하는 트리
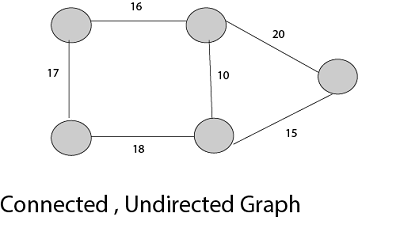
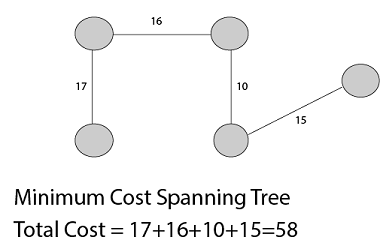
대표적인 MST 알고리즘 종류
- Kruskal’s algoritm(크루스 칼의 알고리즘)
- Prim algorithm(프라임/프림 알고리즘)
Kruskal’s algoritm (크루스 칼의 알고리즘)
- 최적의 솔루션을 찾는 탐욕스러운 접근 방식
- 연결된 그래프와 무 방향 그래프가 주어지면 해당 그래프의 스패닝 트리는 트리이고 모든 정점을 함께 연결하는 하위 그래프
- 스패닝 트리의 가중치는 스패닝 트리의 각 가장자리에 지정된 가중치의 합계
- 시간복잡도 : O (ElogE) 또는 O (ElogV)
연산
- MST에 이미 포함 된 정점을 추적하는 MST 세트를 만듦
- 입력 그래프의 모든 정점에 키 값을 할당. 모든 키 값을 INFINITE (∞)로 초기화. 첫 번째 정점에 0과 같은 키 값을 할당하여 먼저 선택 되도록 함
- 오름차순으로 모든 edge 정렬
- 가장 작은 edge를 선택 후, 지금까지 형성된 스패닝 트리와 함께 사이클을 형성하는지 확인
- 사이클이 형성되지 않은 경우, edge 포함시키고 그렇지 않은 경우에는 edge 버리기
- 스패닝 트리에 (V-1) 가장자리가 있을 때까지 2 ~ 3단계를 반복
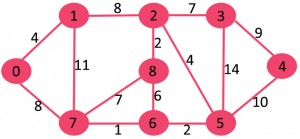
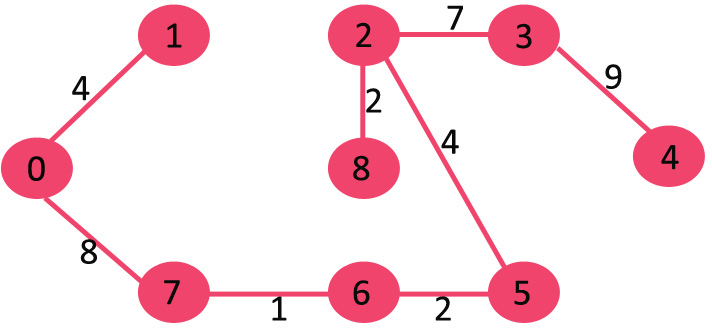
java로 kruskal 알고리즘 구현
Prim algorithm(프라임/프림 알고리즘)
- greedy 알고리즘
- 빈 스패닝 트리로 시작
- 모든 정점이 연결 되어야 함
- 그래프의 모든 정점을 포함하는 가장자리의 하위 집합을 찾아 가장자리 가중치의 합을 최소화를 구하는 알고리즘
- 시간복잡도 : O(E2)
- 인접리스트를 사용할 경우 시간복잡도 : O(ElogV)
- 현재 연결된 노드들을 가장 작은 가중치를 선택해서 찾아가는 과정
연산
- MST에 이미 포함 된 정점을 추적하는 MST 세트를 만듦
- 입력 그래프의 모든 정점에 키 값을 할당. 모든 키 값을 INFINITE (∞)로 초기화. 첫 번째 정점에 0과 같은 키 값을 할당하여 먼저 선택 되도록 함
- 첫번 쨰 정점(vertex)을 선택
- 선택된 정점의 연결된 모든 edge의 값을 오름차순으로 정렬 후 작은 weight 를 선택하여 연결
- 지금까지 형성된 스패닝 트리와 함께 사이클이 형성되는지 확인
- 사이클이 형성되지 않은 경우, edge 포함시키고 그렇지 않은 경우에는 edge 버리기
- 정점에 연결된 모든 edge를 대상으로 3-5단계 반복
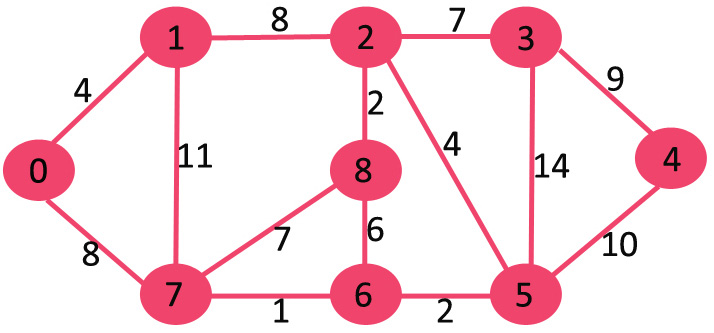
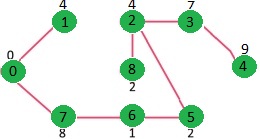
java로 prim 알고리즘 구현
참고 : Union-Find algorithm (유니온-파인드 알고리즘)
- Disjoint Set (서로소 집합) 만들기 : 서로소 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조로 두 개의 유용한 연산을 제공
- 유니온(Union): 두 개의 집합을 하나의 집합으로 합침
- 파인드(Find): 어떤 원소가 주어졌을 때 이 원소가 속한 집합을 반환. find는 일반적으로 어떤 원소가 속한 집합을 “대표” 하는 원소를 반환하는데, 이를 위하여 어떤 원소와 각 대표 원소들 간의 파인드 결과를 비교하여 같은 집합임을 판단
- kruskal 알고리즘에서 사용됨 : 싸이클이 안 생기는 edge 찾아 set을 합치는 과정에서 사용 됨 (싸이클이 생기면 해당 edge 버림)
- find : 새로 연결할 노드가 기존 집합안에 존재하면 싸이클이 생기게 되므로, 이를 버리고 새로운 집합 노드set을 찾는 과정
- union : 싸이클이 생기지 않는 집합의 원소들끼리 하나의 집합으로 합쳐지는 과정
union-by-rank 기법
- Union-Find 구현 기법 중 하나
- rank가 다른 트리가 붙을 때 : 항상 작은 트리를 큰 트리 루트에 붙이는 방법 트리의 깊이(depth)가 실행 시간에 영향을 주기 때문에, depth가 적은 트리를 깊이가 더 깊은 트리의 루트 아래에 추가 함
- rank가 같은 트리가 붙을 때 : 두 트리의 깊이가 같을 경우에만 깊이가 증가
- 최악의 경우 시간복잡도 : O(log n)
references
https://www.javatpoint.com/minimum-spanning-tree-introduction
https://www.javatpoint.com/kruskals-minimum-spanning-tree-algorithm
https://www.javatpoint.com/kruskal-algorithm
https://www.javatpoint.com/prim-algorithm
https://www.javatpoint.com/prims-minimum-spanning-tree-algorithm
https://www.geeksforgeeks.org/applications-of-minimum-spanning-tree/
https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/?ref=lbp
https://www.geeksforgeeks.org/prims-minimum-spanning-tree-mst-greedy-algo-5/
https://www.tutorialspoint.com/data_structures_algorithms/spanning_tree.htm
https://ko.wikipedia.org/wiki/%EC%84%9C%EB%A1%9C%EC%86%8C_%EC%A7%91%ED%95%A9_%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0