[Algorithm] 검색(Search) - 선형 검색, 이진 검색 정의 및 구현

Search (검색) - Linear Search (선형 검색), Binary Search (이진 검색)

• 순서화된 리스트(ordered list)에서 어떤 원소의 위치 및 존재유무를 찾는 것
• 탐색문제의 해 또는 결과 : 원소의 위치
• 보통, 자료구조 형태에 따라 구분됨

검색이 수행되는 장소에 따라 구분

• Internal Search : 적은 양의 레코드를 주기억 장치 내부의 배열이나 연결 리스트 등과 같은 테이블에 적재하여 검색하는 방식
• External Search : 보조기억 장치인 디스크상에 있는 파일로부터 원하는 레코드를 검색하는 방식

내부 검색 방법 구분

• 키 비교에 의한 탐색 방법 : 순차 검색, 이진 검색, 이진 트리 검색, 피보나치 검색, 블록 검색
• 키 변환에 의한 검색 방법 : 해싱

검색 종류

• Linear Search (선형 탐색) = Sequential Search (순차 검색)
• Binary Search (이진 검색)

Linear Search (선형 검색) = Sequential Search (순차 검색)

• 일괄처리 작업 (batch processing operation) 에 사용 됨

장점

• 다음번 레코드에 빠른게 접근 처리 가능
• sort key로 선택하여 정렬작업을 거쳐 순차 파일 편리하게 사용 가능
• 파일내에 여백이 생기지 않아 저장 매체의 효율이 가장 높음

단점

• 삽입, 삭제, 수정등의 update 작업에 파일 전체 복사하는 과정이 필요하기 때문에 수행시간이 오래 걸림

연산

1. arr []의 가장 왼쪽 요소부터 시작하여 arr []의 각 요소와 x를 하나씩 비교
2. x가 요소와 일치하면 인덱스를 반환
3. x가 어떤 요소와도 일치하지 않으면 -1을 반환

java로 선형 탐색 구현

전체소스보기

public static int linearSearch(int arr[], int x) {
    int n = arr.length;

    //순차적으로 arr[]각 요소와 x를 하나씩 비교  
    for (int i = 0; i < n; i++) {
		// 일치할경우 인덱스 반환
        if(arr[i]==x) {
            return i;
        }
    }
   //일치하지 않을 경우 -1 반환
    return -1;
}

Complexity

Complexity	Best Case	Average Case	Worst Case
Time	O(1)	O(n)	O(n)
Space			O(1)

Binary Search (이진 검색)

• Divide and Conquer 알고리즘

연산

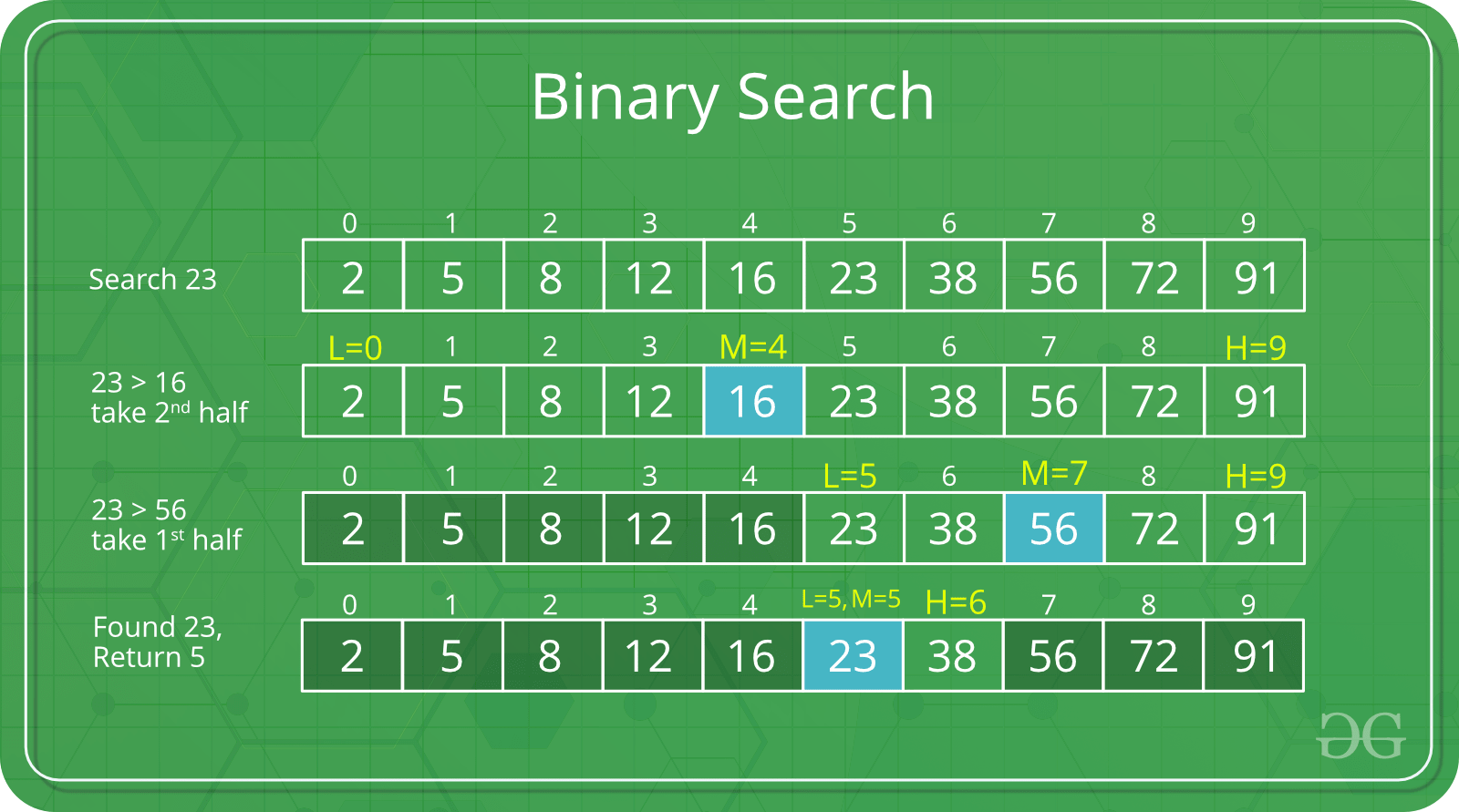
1. x를 중간 요소와 비교
2. x가 중간 요소와 일치하면 중간 인덱스를 반환
3. x가 중간 요소보다 크면 x는 중간 요소 다음의 오른쪽 절반 하위 배열에만 놓고, 오른쪽 절반을 반복
4. 그렇지 않으면 (x는 작음) 왼쪽 절반에 반복

java로 이진 검색 구현

전체소스보기

• 반복문을 이용한 binary search

public static int binarySearch(int[] arr, int x) {
    int left = 0;
    int right = arr.length -1;

    //왼쪽위치가 오른쪽 위치보다 커질때까지 반복
    while (left <= right) {
        //중간요소 위치 계산
        int mid = left + (right-left)/2;

        // 중간 요소와 일치하면 중간 인덱스를 반환
        if(arr[mid] == x) {
            return mid;
        }

        // x가 중간 요소보다 클 경우
        if(arr[mid] < x) {
            // 중간 요소 다음의 오른쪽 절반 하위 배열에만 놓고, 오른쪽 절반을 반복
            // 왼쪽 위치 재조정
            left = mid + 1;

        // x가 중간 요소 보다 작은 경우
        }else {
            // 왼쪽 절반 하위 배열만 놓고, 왼쪽 절반에 반복
            // 오른쪽 위치 재조정
            right = mid - 1;
        }
    }
    //찾을수 없을 경우 -1 반환
    return -1;
}

• recursion을 이용한 binary search

public static int binarySearchRecursion(int[] items, int target, int begin, int end){
    if(begin > end){
        return -1;
    }else {
        int middle = (begin+end)/2;
        int compResult = Integer.toString(target).compareTo(Integer.toString(items[middle]));

        if (compResult == 0){
            return middle;
        } else if (compResult<0){
            return binarySearchRecursion(items, target, begin, middle-1);
        } else {
            return binarySearchRecursion(items, target, middle+1, end);
        }
    }
}

• output

[ * Binary Search * ]
- elements ----------
[1,2,3,4,5,6,7,8,9]
search  : 8
4 6 7 Element is present at index 7
- Binary Search using Recursion ----------
4 6 7 Element is present at index 7

Complexity

Complexity	Best Case	Average Case	Worst Case
Time	O(1)	O(log n)	O(log n)
Space			O(1)

---

references

https://www.javatpoint.com/linear-search
https://www.javatpoint.com/binary-search
https://www.geeksforgeeks.org/linear-search/
https://www.geeksforgeeks.org/binary-search/
https://www.youtube.com/watch?time_continue=1558&v=Vwfo_hrxuzg&feature=emb_title