[Algorithm] 최단경로 (Shortest Path) - 다익스트라(Dijkstra)
Shortest Path (최단 경로 알고리즘)
최단 경로 알고리즘
- 가중치 그래프(Weighted Graph)에서 한 정점에서 다른 정점으로 갈때, 가중치 합이 최소가 되도로 하는 경로를 찾는 알고리즘
- G = (V, E)
최단 경로 알고리즘 종류
Single - source shortest path problem (단일 출발 최단 경로 문제)
- 주어진 정점 u에서 가장 짧은 경로를 찾아야하는 문제
Single - destination shortest paths problem (단일 도착 최단 경로 문제)
- 모든 정점에서 주어진 목적지 정점 v까지의 최단 경로를 찾는 문제
- 그래프에서 각 모서리의 방향을 이동하여 이 문제를 single - source problem(단일 출발 문제) 으로 단축 가능
All - pairs shortest paths problem (전체 쌍 최단 경로 문제)
- 모든 정점 (u, v) 쌍에 대해 u에서 v까지의 최단 경로를 찾는 문제
- 각 정점에서 한 번만 single - source algorithm(단일 출발 알고리즘)을 실행하면이 문제를 명확히 할 수 있음
Dijkstra 알고리즘
- Single - source shortest path problem (단일 출발 최단 경로 문제)
- 주어진 source 정점에서 모든 정점까지의 최단 경로를 찾아내야 하는 문제
- Graph 알고리즘
- “가장 가벼운”또는 “가장 가까운” 꼭지점을 선택하여 최단경로문제를 해결하는 greedy algorithm
- MST(Minimum Spanning Tree) 대한 Prim algorithm 과 매우 유사
- 너비 우선탐색(BFS)와 유사
- 주어진 소스를 루트로 사용하여 SPT (최단 경로 트리) 를 생성
- 시간복잡도 : O (ElogE) ( E : edge의 수)
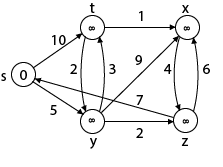
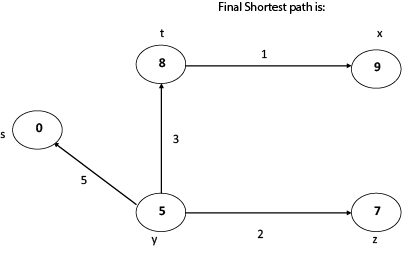
Dijkstra 알고리즘의 단점
- 블라인드 검색을 수행하므로 처리하는 동안 많은 시간을 낭비
- 음의 가장자리를 처리 못 함
- 비순환 그래프로 이어지며 가장 자주 올바른 최단 경로를 얻을 수 없음
- 방문한 정점을 추적을 해야 함
연산
- 각 정점위 위에 시작 점으로 부터 자신에게 이르는 경로의 길이를 무한대로 초기화
- 시작 정점의 경로길이를 0으로 초기화 하고 최단 경로에 추가
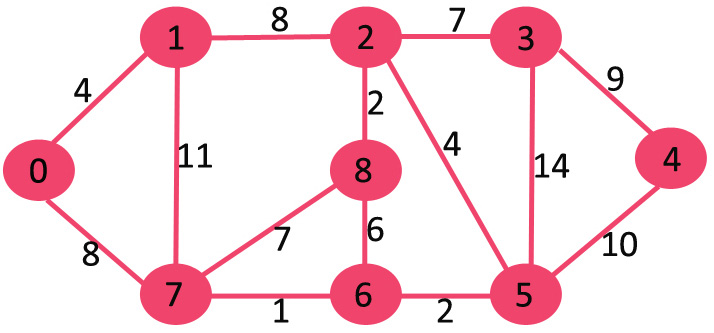
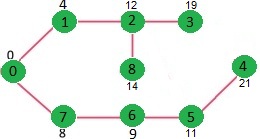
자바를 이용하여 shortest path - Dijkstra algorithm 구현
/**
* 인접행렬로 계산하는 dijsktra
* @param graph
* @param src
*/
public void dijsktra(int graph[][], int src) {
//결과를 담을 배열 distnadce
int distance[] = new int[V];
//shortest path 구했는지 여부
Boolean sptSet[] = new Boolean[V];
//초기화
for (int i = 0; i < V; i++) {
//infinite는 max_value로 셋팅 = 2147483647
distance[i] = Integer.MAX_VALUE;
//최단경로 구하지않았으니 false
sptSet[i] = false;
}
toString(distance);
System.out.println();
// source 정점에서 자기자신까지의 거리는 언제나 0
distance[src] = 0;
//최단경로 찾기
for (int count = 0; count < V-1; count++) {
//distance배열에서 최단경로를 못찾은 정점을 index를 찾아 u에 저장
int u = minDistance(distance, sptSet);
System.out.println( count + ". " + u + " 까지의 최단경로 찾기");
//선택된 점정에서 최단경로를 찾을 것이기 때문에 자기자신은 true로 변경해두어야함
sptSet[u] = true;
for (int v = 0; v < V; v++) {
System.out.println( " ." + v + " : " + sptSet[v] + " " + graph[u][v] + " + " + distance[u] + " < " + distance[v] );
// 1. !sptSet[v] ; false = 최단경로 아직 못찾은 vertex
// 2. graph[u][v] != 0 ; u에서 v까지의 엣지가 있어야함 ( 거리가 0 아니여야함 )
// 3. 최단경로를 찾으려는 정점이 현재 경로가 infinite 가 아니여아 함
// 4. (((distance[u] + graph[u][v]) < distance[v])) ; src에서 v에서 u까지의 총 경로 가중치 < distance [v]의 현재 값보다 작아야 함
if (!sptSet[v] && (graph[u][v] != 0) && (distance[u] != Integer.MAX_VALUE) && (((distance[u] + graph[u][v]) < distance[v]))) {
//결과값에 최단경로 update 해주기
distance[v] = distance[u] + graph[u][v];
System.out.println(" * result : " + distance[v] + " <= " + distance[u] + " + " + graph[u][v] );
}
}
}
toString(distance);
}
/**
* 최단경로 못찾은 정점 찾기
* @param distance
* @param sptSet
* @return
*/
public int minDistance(int[] distance, Boolean[] sptSet) {
//최소값 초기화
int min = Integer.MAX_VALUE;
int min_index = -1;
System.out.println("최단경로 못찾은 정점 찾기");
for (int v = 0; v < V; v++) {
// 결과배열 0~9까지 최단경로를 찾지못했고, 배열이 초기값(infinite)값과 같거나 작으면
if (sptSet[v] == false && distance[v] <= min) {
//아직 최단경로를 찾지 못한 정점임
System.out.println("" + v + " : " + distance[v]);
min = distance[v];
min_index = v;
//for문을 다 돌렸을 때, 최소값 인덱스가 나오게 되어있음
}
}
//최단경로 못 찾은 인덱스 return
return min_index;
}
output
Vertex Distance from Source
0 2147483647
1 2147483647
2 2147483647
3 2147483647
4 2147483647
5 2147483647
6 2147483647
7 2147483647
8 2147483647
최단경로 못찾은 정점 찾기
0 : 0
0. 0 까지의 최단경로 찾기
.0 : true 0 + 0 < 0
.1 : false 4 + 0 < 2147483647
* result : 4 <= 0 + 4
.2 : false 0 + 0 < 2147483647
.3 : false 0 + 0 < 2147483647
.4 : false 0 + 0 < 2147483647
.5 : false 0 + 0 < 2147483647
.6 : false 0 + 0 < 2147483647
.7 : false 8 + 0 < 2147483647
* result : 8 <= 0 + 8
.8 : false 0 + 0 < 2147483647
최단경로 못찾은 정점 찾기
1 : 4
1. 1 까지의 최단경로 찾기
.0 : true 4 + 4 < 0
.1 : true 0 + 4 < 4
.2 : false 8 + 4 < 2147483647
* result : 12 <= 4 + 8
.3 : false 0 + 4 < 2147483647
.4 : false 0 + 4 < 2147483647
.5 : false 0 + 4 < 2147483647
.6 : false 0 + 4 < 2147483647
.7 : false 11 + 4 < 8
.8 : false 0 + 4 < 2147483647
최단경로 못찾은 정점 찾기
2 : 12
7 : 8
2. 7 까지의 최단경로 찾기
.0 : true 8 + 8 < 0
.1 : true 11 + 8 < 4
.2 : false 0 + 8 < 12
.3 : false 0 + 8 < 2147483647
.4 : false 0 + 8 < 2147483647
.5 : false 0 + 8 < 2147483647
.6 : false 1 + 8 < 2147483647
* result : 9 <= 8 + 1
.7 : true 0 + 8 < 8
.8 : false 7 + 8 < 2147483647
* result : 15 <= 8 + 7
최단경로 못찾은 정점 찾기
2 : 12
6 : 9
3. 6 까지의 최단경로 찾기
.0 : true 0 + 9 < 0
.1 : true 0 + 9 < 4
.2 : false 0 + 9 < 12
.3 : false 0 + 9 < 2147483647
.4 : false 0 + 9 < 2147483647
.5 : false 2 + 9 < 2147483647
* result : 11 <= 9 + 2
.6 : true 0 + 9 < 9
.7 : true 1 + 9 < 8
.8 : false 6 + 9 < 15
최단경로 못찾은 정점 찾기
2 : 12
5 : 11
4. 5 까지의 최단경로 찾기
.0 : true 0 + 11 < 0
.1 : true 0 + 11 < 4
.2 : false 4 + 11 < 12
.3 : false 14 + 11 < 2147483647
* result : 25 <= 11 + 14
.4 : false 10 + 11 < 2147483647
* result : 21 <= 11 + 10
.5 : true 0 + 11 < 11
.6 : true 2 + 11 < 9
.7 : true 0 + 11 < 8
.8 : false 0 + 11 < 15
최단경로 못찾은 정점 찾기
2 : 12
5. 2 까지의 최단경로 찾기
.0 : true 0 + 12 < 0
.1 : true 8 + 12 < 4
.2 : true 0 + 12 < 12
.3 : false 7 + 12 < 25
* result : 19 <= 12 + 7
.4 : false 0 + 12 < 21
.5 : true 4 + 12 < 11
.6 : true 0 + 12 < 9
.7 : true 0 + 12 < 8
.8 : false 2 + 12 < 15
* result : 14 <= 12 + 2
최단경로 못찾은 정점 찾기
3 : 19
8 : 14
6. 8 까지의 최단경로 찾기
.0 : true 0 + 14 < 0
.1 : true 0 + 14 < 4
.2 : true 2 + 14 < 12
.3 : false 0 + 14 < 19
.4 : false 0 + 14 < 21
.5 : true 0 + 14 < 11
.6 : true 6 + 14 < 9
.7 : true 7 + 14 < 8
.8 : true 0 + 14 < 14
최단경로 못찾은 정점 찾기
3 : 19
7. 3 까지의 최단경로 찾기
.0 : true 0 + 19 < 0
.1 : true 0 + 19 < 4
.2 : true 7 + 19 < 12
.3 : true 0 + 19 < 19
.4 : false 9 + 19 < 21
.5 : true 14 + 19 < 11
.6 : true 0 + 19 < 9
.7 : true 0 + 19 < 8
.8 : true 0 + 19 < 14
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
references
https://en.wikipedia.org/wiki/Shortest_path_problem
https://www.javatpoint.com/single-source-shortest-paths
https://www.javatpoint.com/dijkstras-algorithm
https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/
https://www.tutorialspoint.com/design_and_analysis_of_algorithms/design_and_analysis_of_algorithms_shortest_paths.htm