[Algorithm] 정렬(Sort)-힙 정렬(Heap Sort)

정렬(Sort) - 힙 정렬(Heap Sort)

Heap Sort(힙 정렬)

• 내부정렬 알고리즘
• 키를 비교하여 선택에 의하여 정렬하는 선택방식 정렬
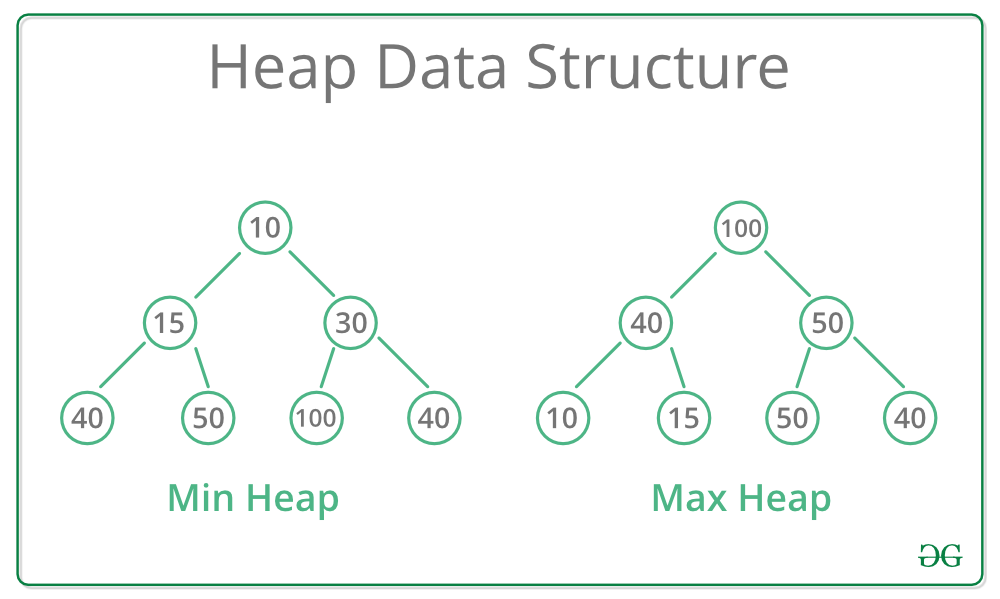
• Max-Heap(최대 힙) : 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 커야 함
• Min-Heap(최소 힙) : 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 최소 여야 함
• 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로서, 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성
• 최대값 혹은 최소값을 빠르게 찾아야하는데 사용 됨
• complete binary tree¹로 구성
• heapify : heap속성을 충족하기 위해, 힙의 위치를 ​​조정하는 과정

연산

1. 삽입의 경우, complete binary tree로 루트 노드부터 부모노드, 왼쪽 자식노드, 오른쪽 자식노드 순으로 구성하며 채움
2. 최대 힙인 경우, root node가 가장 커야 하며, parent node가 child node 보다 작을 경우 교환 heapify
3. 최소 힙인 경우, root node가 가장 작아야 하며, parent node가 child node 보다 클 경우 교환 heapify
4. 삭제의 경우, 는 root를 삭제하는 것이 일반적으로, 맨 마지막에 위치한 node를 root로 올리고 child node보다 큰/작을 경우 교환 heapify
5. heapfiy 과정이 끝나면 정렬
6. 최대 힙인 경우, root node(=array[0])가 가장 큰 값 임으로 맨 뒤에 있는 요소와 교환 후 heapify 반복하면 오름차순 정렬 됨
7. 최소 힙인 경우, root node(=array[0])가 가장 작은 값 임으로 맨 앞에 있는 요소와 교환 후 heapify 반복하여 내림차순 정렬 됨

입력 data: 4, 10, 3, 5, 1
괄호안에 숫자는 index
         4(0)
        /   \
     10(1)   3(2)
    /   \
 5(3)    1(4)


인덱스 1에 heapify 프로 시저 적용 :
         4(0)
        /   \
    10(1)    3(2)
    /   \
5(3)    1(4)


인덱스 0에 heapify 프로 시저 적용 :
        10(0)
        /  \
     5(1)  3(2)
    /   \
 4(3)    1(4)

heapify 프로시저는 하향식으로 힙을 빌드하기 위해 재귀 적으로 호출 됨

java로 힙 정렬 구현

• heap은 array로 구현
• root는 index는 array[0]
• index of parent node = array[(i-1)/2]
• index of the left child node = array[(2*i)+1]
• index of the right child node = array[(2*i)+2]

전체소스보기

    /**
     * heap sort 구현
     * @param arr
     */
    public static void sort(int[] arr) {
        int n = arr.length;

        // [build heap] 요소들을 heapify 해주기
        // i = tree의 level이 됨 (i= 3 ~ 0 까지)
        for (int i = n/2-1; i>=0; i--) {
            heapify(arr, n, i);
        }

        System.out.println();
        System.out.println("-  max heapify  ----------");
        System.out.println(toString(arr));

        System.out.println();
        System.out.println("- get sorted array  ----------");

        // 0. 힙을 빌드 한 후, max 요소는 힙의 루트에 있음 (root의 값은 array[0]으로 제일 큰 값이 됨 )
        // 1. max 요소를 (n - 1) 번째 위치로(오름차순을 위해 맨 뒤) 교환
        // 2. 가장 큰 요소가 적절한 위치에 있고, n 크기를 줄여 힙에서 제거
        // 3. 가장 큰 요소를 교환하면 max heap 속성을 방해 할 수 있으므로 다시 heapify
        // 4. 힙에 요소가 남지 ​​않을 때까지 위의 단계를 수행 하면 결국 정렬 된 배열을 얻게 됨
        for (int i = n-1; i > 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            heapify(arr, i, 0);
            System.out.println(toString(arr));
        }
    }

    /**
     * heapify : heap속성을 충족하기 위해, 힙의 위치를 ​​조정하는 과정
     * 1. max heap 생성하기 위해 현재 요소를 하위 요소와 비교하여 최대 값을 찾은 후
     * 2. 현재 요소가 최대 값이 아닌 경우 최대 값이 위치한 왼쪽 또는 오른쪽 하위 요소로 교환
     * @param arr
     * @param n
     * @param i
     */
    public static void heapify(int arr[], int n, int i) {
        int largest = i; // parent node
        int left = 2*i + 1; // left node = 2*i + 1
        int right = 2*i + 2; // right node = 2*i + 2

        // left의 크기가 array 사이즈 내에 존재 하면서
        // 왼쪽 노드이 값 > 부모노드의 값을 비교 하여 큰 경우
        if(left < n && arr[left] > arr[largest]) {
            //largest index에 left index값을 넣어 줌 (부모노드가 될 것임)
            largest = left;
        }

        // right의 크기가 array 사이즈 내에 존재하면서
        // 오른쪽 노드의 값이 > 부모 노드의 값과 비교하여 큰 경우
        if (right < n && arr[right] > arr[largest]) {
            //largest index에 right index값을 넣어 줌  (부모노드가 될 것임)
            largest = right;
        }

        //자식 노드의 값이 부모노드 보다 큰 값이 존재 할 경우,
        // largest 값이 변경 되었으므로
        if (largest != i) {
            // 부모노드와 <-> 자식노드 swap   
            // 임시변수에 기존 parent node 를 저장하고
            int temp = arr[i];
            // 부모 노드를 자식 노드 들 중에 컸던 값으로 대체  
            arr[i] = arr[largest];
            // 자식노드에 부모값 저장
            arr[largest] = temp;

            //[순환] 바뀐 largest를 기준으로 다시 heapify
            heapify(arr, n, largest);
        }
    }

• output

[ * Heap Sort * ]
- before heap sort ----------
[9,5,6,4,7,2,1,8,3]

-  max heapify  ----------
[9,8,6,5,7,2,1,4,3]

- get sorted array  ----------
[8,7,6,5,3,2,1,4,9]
[7,5,6,4,3,2,1,8,9]
[6,5,2,4,3,1,7,8,9]
[5,4,2,1,3,6,7,8,9]
[4,3,2,1,5,6,7,8,9]
[3,1,2,4,5,6,7,8,9]
[2,1,3,4,5,6,7,8,9]
[1,2,3,4,5,6,7,8,9]

- after heap sort ----------
[1,2,3,4,5,6,7,8,9]

Complexity

Complexity	Best Case	Average Case	Worst Case
Time	Ω(nlogn)	θ(nlogn)	O(nlogn)
Space			O(1)

• heapify 의 시간복잡도도 : O(logn)

---

references

https://www.javatpoint.com/heap-sort
https://www.geeksforgeeks.org/heap-data-structure/

---

주석

1. 마지막 level을 제외하고 모든 level이 완전히 채워지고 마지막 level에 가능한 한 왼쪽에 모든 키가 있는 경우 ↩