[Algorithm] 정렬(Sort)-병합 정렬(Merge Sort)

정렬(Sort) - 병합정렬(Merge Sort)

merge sort (병합 정렬)

• Divide and Conquer 알고리즘
• 여러 개의 정렬되어있는 배열 자료들을 혼합하여 하나의 정렬된 배열로 합치는 작업
• 재귀 용법 사용

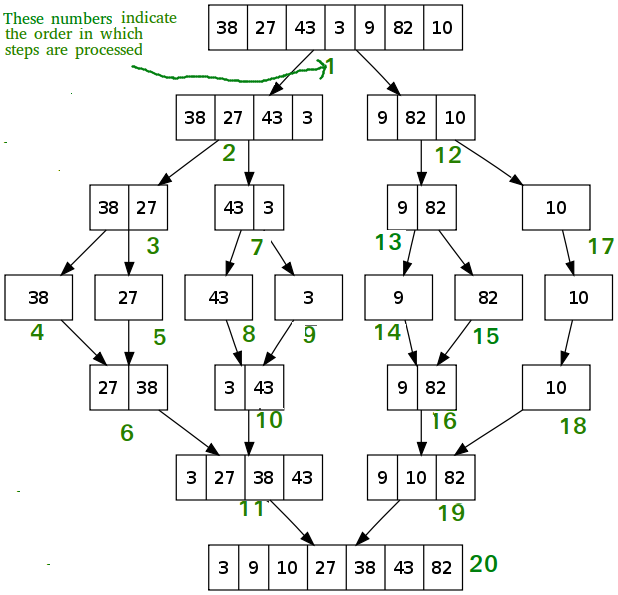
연산

1. 리스트의 길이가 1 이하이면 이미 정렬된 것으로 보고, 그렇지 않은 경우에
2. 분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눔
3. 정복(conquer) : 각 부분 리스트를 재귀적으로 병합 정렬을 이용해 정렬
4. 결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 병합. 이때 정렬 결과가 임시배열에 저장 됨
5. 복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사

java로 병합 정렬 구현

전체소스보기

    /**
     * 정렬
     * @param arr
     * @param left
     * @param right
     */
    public static void sort(int[] arr, int left, int right) {
        if (left < right) {
            //(분할) 중앙요소 위치 찾기
            int mid = (left + right) /2;

            //(정렬) 앞 부분 : left (0) ~ mid / 뒷 부분 : mid+1 ~ right (n) 까지  
            sort(arr, left, mid);  
            sort(arr, mid+1 , right);

            //(병합)
            merge(arr, left, mid, right);
        }
    }

    /**
     * 병합
     * 첫번째 서브array array[left..mid]
     * 두번째 서브array array[mid+1..right]
     * @param arr
     * @param left
     * @param mid
     * @param right
     */
    public static void merge(int[] arr, int left, int mid, int right) {

        //병합될 두 sub arrays 의 사이즈 찾기
        int n1 = mid - left + 1 ;
        int n2 = right - mid;

        // (복사) mid를 기준으로 왼쪽 / 오른쪽 2개 파트로 나눌 임시 배열 생성
        // 또는 arr에 대한 임시 배열을 만들어서 넣어주고, 병합 후 임시배열을 arr 복사해서 넣어주어도 됨
        int L[] = new int[n1];
        int R[] = new int[n2];

        // 임시 배열값 복사
        for (int i = 0; i < n1; i++) {
            L[i]  = arr[left + i];
        }

        for (int j = 0; j < n2; j++) {
            R[j] = arr[mid + 1 + j];
        }

        //merge
        //초기 인덱스
        int i = 0;
        int j = 0;

        // 병합된 subarray의 초기 인덱스
        int k = left;

        // L 사이즈만 큼 loop (L배열 초기 인덱스 < L배열 사이즈)
        // R 사이즈만 큼 loop (R배열 초기 인덱스 < R배열 사이즈)  
        while (i < n1 && j < n2) {
            // L 배열의 값 <= R배열의 값
            if (L[i] <= R[j]) {
                // L값 arr에 담아주기
                arr[k] = L[i];
                //L 을 담아주었으니 L의 인덱스 증가
                i++;
            }else {
                // L 배열의 값 > R배열의 값
                // R값 arr에 담아주기
                arr[k] = R[j];
                //R 을 담아주었으니 R의 인덱스 증가
                j++;
            }
            k++;
        }

        //L에 남은 값이 있다면 복사
        while(i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        //R에 남은 값이 있다면 복사  
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }

    }

• output

[ * Merge Sort * ]
- before merge sort ----------
[38,27,43,3,9,82,10]
- sorting ----------
left right mid : [LEFT] , [RIGHT]  -->  [SORTED]
0 0 1 : [38] [27]                  -->  [27,38,43,3,9,82,10]
2 2 3 : [43] [3]                   -->  [27,38,3,43,9,82,10]
0 1 3 : [27,38] [3,43]             -->  [3,27,38,43,9,82,10]
4 4 5 : [9] [82]                   -->  [3,27,38,43,9,82,10]
4 5 6 : [9,82] [10]                -->  [3,27,38,43,9,10,82]
0 3 6 : [3,27,38,43] [9,10,82]     -->  [3,9,10,27,38,43,82]
- after merge sort ----------
[3,9,10,27,38,43,82]

Complexity

• 각 단계는 O(n)
• 단계는 항상 O(log n) 만큼 생성
• 전체는 O(n)* O(log n) = O(n log (n))

Complexity	Best Case	Average Case	Worst Case
Time	O(n log n)	O(n log n)	O(n log (n))
Space			O(n)

---

references

https://www.javatpoint.com/merge-sort
https://www.geeksforgeeks.org/merge-sort/
https://www.tutorialspoint.com/data_structures_algorithms/merge_sort_algorithm.htm