[Algorithm] 정렬(Sort)-퀵 정렬(Quick Sort)

정렬(Sort) - 퀵 정렬(Quick Sort)

Quick Sort(퀵 정렬)

• Divide and Conquer 알고리즘
• 평균수행능력이 가장 뛰어남
• 분할중심값을 pivot 또는 control key 라고 함

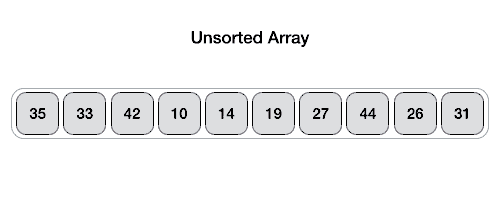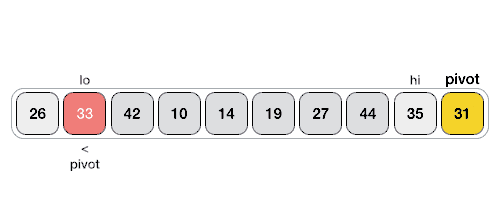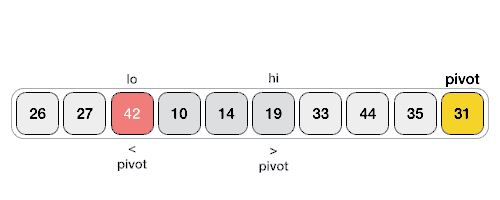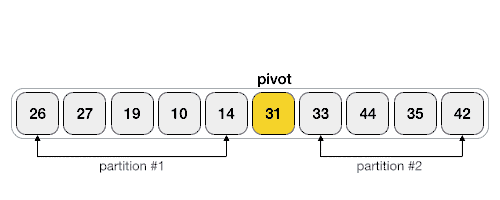
연산

1. 피벗값을 선택(맨 오른쪽, 왼쪽 또는 중앙값을 선택)
2. 피벗 값을 사용하여 배열 분할
3. 파티션 자료 갯수가 1이 될때까지 왼쪽 파티션을 재귀로 빠르게 정렬
4. 파티션 자료 갯수가 1이 될때까지 오른쪽 파티션을 재귀로 빠르게 정렬

pseudo code

quickSort(arr[], low, high)
{
    if (low < high)
    {
        pi = partition(arr, low, high);

        quickSort(arr, low, pi );  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

partition (arr[], low, high)
{
    pivot = arr[(low+high)/2];  

    while(arr[left]<pivot){
        left++
    }

    while(arr[right]>pivot){
        right--
    }

    if (left <= right){
        swap(arr[left],arr[right])
        left++
        right--
    }

    return right
}

java로 퀵 정렬 구현

전체소스보기

public static void sort(int[] arr, int start, int end) {
    //int pivot = arr[end];
    int left = start;
    int right = end ;

    // pivot값을 가운데 값으로 셋팅
    int pivot = arr[(left+right)/2];
    while( left <= right) {

        //pivot 왼쪽의 값이  pivot 값 보다 작은 경우 다음 element 탐색
        while(arr[left] < pivot) {
            left++;
        }

        // pivot 오른쪽의 값이 pivot값 보다 큰 경우 다음 element 탐색
        while(arr[right] > pivot) {
            right--;
        }

        //왼쪽 값 > pivot 이면서
        //오른쪽 값 < pivot 이면서
        //왼쪽값 < 오른쪽 값 인 경우
        if( left <= right) {
            //swap
            int temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;

            //그리고 다음 element 탐색
            left++;
            right--;
        }
    }

    if (start < right ) {
        // 분할된 왼쪽 부분 순환 처리
        sort(arr, start, right);
    }

    if (left < end ) {
        // 분할된 오른쪽 부분 순환 처리
        sort(arr, left, end);
    }
}

• output

[ * Quick Sort * ]
- before quick sort ----------
[9,5,6,4,7,2,1,8,3]
- sorting ----------
[9,5,6,4,7,2,1,8,3]
[3,5,6,4,1,2,7,8,9]
[3,5,2,4,1,6,7,8,9]
[1,2,5,4,3,6,7,8,9]
[1,2,5,4,3,6,7,8,9]
[1,2,3,4,5,6,7,8,9]

Complexity

Complexity	Best Case	Average Case	Worst Case
Time	O(n)	O(n log n)	O(n2)
Space			O(log n)

---

references

https://www.javatpoint.com/quick-sort
https://www.geeksforgeeks.org/quick-sort/?ref=lbp/
https://www.tutorialspoint.com/data_structures_algorithms/quick_sort_algorithm.htm
https://ko.wikipedia.org/wiki/%ED%9E%99_%EC%A0%95%EB%A0%AC
https://codenuclear.com/quick-sort-algorithm/