[Data Structure] 비선형 자료구조(1) - 트리(Tree)

[Data Structure] 비선형 자료구조(1) - 트리(Tree)

• 트리(Tree)
• 그래프(Graph)

Tree

• 각 자료 항목간의 계층관계를 표현하는 자료구조
• 파일 색인기법(file index scheme) 에서 이용
• 계층적 데이터 베이스 시스템(hierarchical database system) 에서 이용
• children이라 부르며 서로 다른 원소를 많이 나열 할 수 있는 자료구조
• 비선형
• 계층형

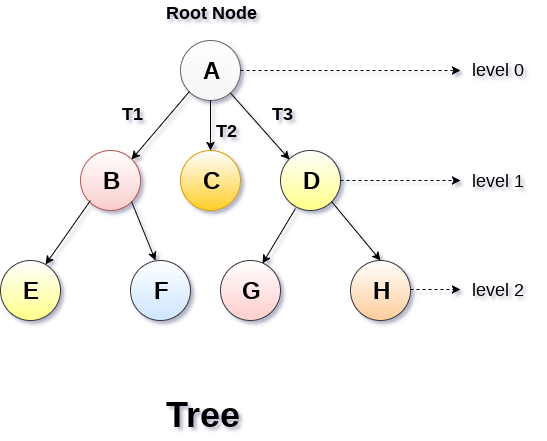
• node (노드) : 트리의 기본 구성 요소. 다른 노드를 연결하기 위하여 사용 하는 branch 포함
• root : 트리의 가장 높은 레벨, 최상위 노드. root의 레벨은 0. 부모가 없는 노드
• depth : 트리의 최대 레벨을 깊이
• level :트리의 각 노드에는 각 노드가 부모보다 한 레벨 높은 레벨에있는 레벨 번호가 할당
• ancestor node : 노드의 조상은 루트에서 해당 노드까지의 경로에있는 모든 선행 노드
• parent node : 어떤 노드의 다음 레벨에 연결된 노드
• child node : 어떤 노드의 상위 레벨에 연결된 노드
• path : 연속적인 가장자리 시퀀스를 경로
• brother, sbiling node : 같은 부모노드를 갖는 자식 노드들의 집합
• subtree : 루트 노드가 null이 아닌 경우 트리 T1, T2 및 T3을 루트 노드의 하위 트리라고 함
• degree of node : 자식 노드의 개수
• degree of tree : 트리를 구성하고 있는 노드 중에서 degree가 가장 큰 것
• leaf node , terminal node : 자식 노드가 없는 트리 노드. 트리의 가장 아래쪽 노드. 일반 트리에는 여러 개의 leaf 노드가 있음. leaf 노드는 외부 노드라고도 함.
• nonterminal node : degree 가 0이 아닌 노드
• forest : 분리된 트리의 집합
• ordered tree : 순서가 중요한 의미를 갖는 트리

Binary Tree (이진트리)

• 가장 기본적인 tree
• 각 element는 최대 2개의 children을 가짐
• 공백일 수도 있음
• 왼쪽 자식노드 다음에 오른쪽 자식노드순으로 순서를 구분하는 ordered tree

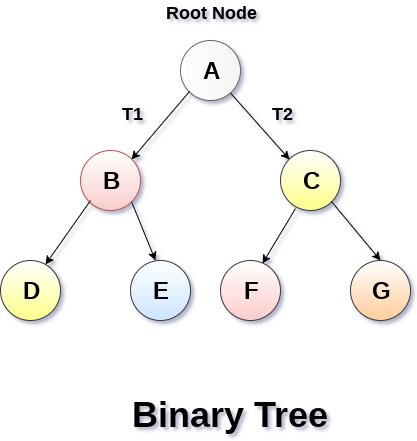
종류

Full Binary Tree

• 모든 노드에 0 또는 2 개의 자식이있는 경우 전체 이진 트리
• leaft 노드를 제외한 모든 노드에 두 개의 자식이 있는 경우 (=모든 내부 노드에 두 명의 자식이 있고 모든 리프 노드가 같은 수준에 있는 경우)

               18
           /       \  
         15         30  
        /  \        /  \
      40    50    100   40


             18
           /    \   
         15     20    
        /  \       
      40    50   
    /   \
   30   50


               18
            /     \  
          40       30  
                   /  \
                 100   40

Complete Binary Tree

• 마지막 level을 제외하고 모든 level이 완전히 채워지고 마지막 level에 가능한 한 왼쪽에 모든 키가 있는 경우
• 예는 binary heap
• 깊이 d를 갖을때, 총 노드 수는 2 ^{d + 1} -1 , 여기서 leaf node는 2^d 이고 non-leaf 노드는 2^d -1입

               18
           /       \  
         15         30  
        /  \        /  \
      40    50    100   40


               18
           /       \  
         15         30  
        /  \        /  \
      40    50    100   40
     /  \   /
    8   7  9

Perfect Binary Tree

• 모든 내부 노드에 두 명의 자식이 있고, 모든 leaf 노드가 같은 level에 있는 경우

               18
           /       \  
         15         30  
        /  \        /  \
      40    50    100   40


               18
           /       \  
         15         30  

Balanced Binary Tree

• n이 노드의 수 일때, 트리의 높이가 O(Log n) 인 경우 균형을 이루는 경우
• 검색, 삽입 및 삭제에 O (log n) 시간을 제공하므로 성능 측면에서 우수
• 예로 AVL 트리는 왼쪽 및 오른쪽 하위 트리의 높이 차이가 거의 1인지 확인하여 O (Log n) 높이를 유지
• 예로 Red-Black 트리는 다음 수를 확인하여 O (Log n) 높이를 유지, 모든 루트에서 leaf 경로까지의 Black 노드는 동일하며 인접한 red 노드는 없음

A degenerate (or pathological) tree

• 모든 내부 노드에 자식이 하나있는 경우
• linked list와 같은 성능
• 깊이가 d 인 이진트리가 d개로 구성 됨

      10
      /
    20
     \
     30
      \
      40     

공간복잡도

• 최악의 경우 O(n)

시간복잡도

Algorithm	Average Case	Worst Case
Access	O(n)	O(n)
Search	O(log n)	O(n)
Insert	O(log n)	O(n)
Delete	O(n)	O(n)

이진트리 운행 (Traversal)

• Pre-order Traversal (전위) : Root -> Left -> Right
  루트를 먼저 순회 한 다음 왼쪽 하위 트리와 오른쪽 하위 트리로 각각 순회. 트리의 각 하위 트리에 재귀 적으로 적용
• In-order Traversal (중위) : Left -> Root -> Right
  왼쪽 하위 트리를 먼저 순회 한 다음 루트 및 오른쪽 하위 트리를 각각 순회. 트리의 각 하위 트리에 재귀 적으로 적용
• Post-order Traversal (후위) : Left -> Right -> Root
  왼쪽 하위 트리를 순회 한 다음 오른쪽 하위 트리와 루트를 각각 순회. 트리의 각 하위 트리에 재귀 적으로 적용

Binary Search Tree (BST : 이진검색트리)

• 순서가 지정된 이진 트리
• binary tree 구현 중 하나
• 주어진 node의 값보다 작은 자식은 왼쪽 하위 트리, 큰 원소는 오른쪽 하위 트리
• 이진 검색 트리는 검색, 정렬 등과 ​​같은 컴퓨터 과학 도메인의 대부분의 응용 프로그램에서 사용 됨

장점

• 검색 프로세스에서 array 및 linked list 과 비교할 때, 모든 단계에서 하위 트리의 반을 제거해서 검색함으로 매우 효율적인 데이터 구조로 간주되며, 효율적으로 검색이 진행 됨
• Binary Search Tree 시간복잡도 : O(logn)
• Binary Search Tree 최악의 경우 : O(n) (최악의 경우는 배열과 시간복잡도가 같게 되는 경우)
• array 및 linked list에 비해서는 삽입 및 삭제 작업 속도가 향상됨

예제

자바로 구현한 이진검색트리 ( binary search tree implementation using JAVA )

전체소스보기

output

Binary search tree after insertion :
Inorder Traversal :
10 20 30 40 50 60 70 80 90

Preorder Traversal :
50 10 20 30 40 60 70 80 90

Postorder Traversal :
10 20 30 40 60 70 80 90 50

Search element :
finding using recursion: 10
not found : 15
finding using while: 80
not found : 85

Get size of  Binary search tree :
9

Find root of Binary search tree :
50

Binary search tree after deleting node 30 :
10 20 40 50 60 70 80 90

Binary search tree after deleting node 60 :
10 20 40 50 70 80 90

Get size of  Binary search tree :
7

AVL (Adelson - Velskii and Landis Tree) 균형잡힌 이진검색트리

• 균형이 맞을때 검색이나, 삽입, 삭제할때 O(log n)의 처리시간 소요
• 어떤 node의 값도 1차이가 넘지 않도록 만듦
• 노드의 균형 계수가 -1에서 1 사이이면 트리는 균형이 잡히고, 그렇지 않으면 트리의 균형이 맞지 않아 균형을 조정 해야 함
• 회전(rotation)을 통해 트리를 재구성하여 높이 균형 성질을 유지

균형 계수 (k) = 높이 (왼쪽 (k))-높이 (오른쪽 (k))

• 노드의 균형 계수가 1 인 경우 왼쪽 하위 트리가 오른쪽 하위 트리보다 한 수준 높음을 의미
• 노드의 균형 계수가 0이면 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같음
• 노드의 균형 계수가 -1이면 왼쪽 하위 트리가 오른쪽 하위 트리보다 한 수준 낮다는 의미
• 각 노드와 관련된 균형 계수가 -1과 +1 사이에 있어야 AVL 트리의 예

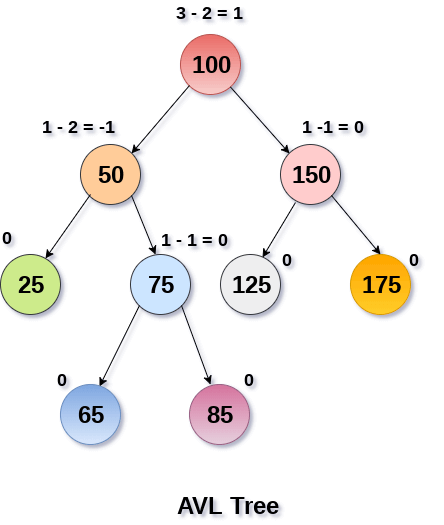
시간복잡도

Algorithm	Average Case	Worst Case
Space	O(n)	O(n)
Search	O(log n)	O(log n)
Insert	O(log n)	O(log n)
Delete	O(log n)	O(log n)

---

references

https://www.javatpoint.com/tree
https://www.javatpoint.com/binary-tree
https://www.javatpoint.com/java-program-to-construct-a-binary-search-tree-and-perform-deletion-and-in-order-traversal
https://www.geeksforgeeks.org/binary-tree-data-structure/
https://www.tutorialspoint.com/data_structures_algorithms/tree_data_structure.htm
https://ko.wikipedia.org/wiki/AVL_%ED%8A%B8%EB%A6%AC